Name the properties of a rectangle.

Why are the diagonals of a square or a rectangle congruent?

During a local math Olympiad the team from Bigtown High School was presented with the following problem to solve in no more than 2 minutes: "What is the relationship between the number of vertices of a regular polygon and the number of symmetry lines of the polygon?" They did it! What was their answer?

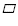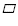The coordinates of PQRS are P(3, 0), Q(-1, 7), R(-5, 0), S(-1, -7). Graph PQRS. Decide whether it is a rectangle, a rhombus, a square, or none of the above. Justify your answer using the theorems about quadrilaterals.

In ABCD, mA=(10x + 85) and mC=(5x + 75). Find the measures of B and D.

In PQRS, mP=(4x + 57) and mR=(7x + 69). Find the value of x.

Brian was messing around with some pattern blocks that were made in various geometric shapes. All the pattern blocks had congruent sides. He joined a hexagon with a nonagon (side to side) to create a new polygon. How many sides did the new polygon have?

Which of the following is NOT a property of a parallelogram?

		Opposite sides are parallel.
		Consecutive angles are supplements.
		Consecutive angles are congruent.
		Opposite sides are congruent.
		Opposite angles are congruent.

When two congruent polygons are joined so that two sides are put together (one side of each polygon is matched with one side of the other polygon) to create a new larger polygon, how many sides does the new polygon have? Explain why your rule works. Consider each original polygon to have n sides.

State whether the figure is a polygon. If it is, identify the polygon and state whether it is convex or concave. If it is not, explain why.